XOR swaps
Swap two variables using XOR operations
14 Jan 2018
View Comments
#xor
#swap
#algorithm
#programming
#bitwise
#operation
 |
XOR swaps algorithm is a technique in programming that uses XOR bitwise operations to swap values of distinct variables having the same data type without using a temporary variable. We commonly swap 2 values which use a temporary variable, like below:
tmp = x
x = y
y = tmpSwapping using temporary variable works perfectly fine. However, there is another trick to swap the variable, XOR swaps algorithm. No temporary storage is needed. The algorithm looks like this:
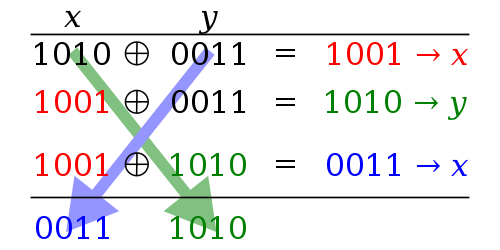
x = x xor y
y = x xor y
x = x xor y |
Here we have 3 machine code instructions calling XOR operations 3 times in sequence. This works regardless of integers or string because numbers or strings can basically be represented in binary numbers in a computer.
Reversing a String
As I mentioned, the algorithm can also be applied to a string for reversing its content because the character is essentially is composed of a set of binary numbers. For example, character ‘a’ is represented as 97 (decimal value) in ASCII, which is same as ‘01100001’ in binary. Most computers typically reserve 1 byte, 8 bits, for an ASCII character so a character is can typically be represented by 256 different values. ASCII, however, do not typically use the first bit which would use only 7 bits to represent 128 different values. The first bit may be used as a parity bit if necessary. The code example in Java is found in my github where the tests are written here OR code snippets are shown below:
public String reverseStringXOR(String s) {
char[] charArray = s.toCharArray();
int start = 0;
int end = charArray.length - 1;
while (start < end) {
charArray[start] ^= charArray[end];
charArray[end] ^= charArray[start];
charArray[start] ^= charArray[end];
++start;
--end;
}
return new String(charArray);
}The trick just isn’t limited to the ASCII, you can apply the same code to swap UTF-8 characters. Using the UTF encoding means that character is represented using 1/2/3/4 bytes length, it doesn’t change the fact the character swaps after using the XOR swaps algorithm. ASCII uses only the first 7 bits of an 8 bit byte. So all combinations from 00000000 to 01111111. All 128 bytes in this range are mapped to a specific character. UTF-8 basically keeps these exact mappings. So trick will work in either unicode or ASCII.
Pitfall / Drawback
Notice how I used the words, distinct variables, to describe the XOR swaps above. The word distinct is important here because it means 2 separate memory locations are used. The values themselves can be the same as long as the location of those values is separate. The algorithm will fail when x and y use the same storage location because the value stored in that location will be zeroed out from the first XOR instruction and then remain zero for the other variable which will eventually fail to swap the value.
When to use
In the past, there have been cases when XOR swaps were necessary. Theoretically, usage of this may be encouraged in a very rigid environment where having the most efficient space complexity is important. In a modern software programming, XOR swaps are rarely needed though because space is abundant and processors are well optimized. You probably rarely find places that still use the XOR swaps.
When not to use
XOR swaps might save the “space” by a fraction. However, this trivial trick isn’t the best solution if you consider maximizing the “time” complexity. On a modern CPU architecture, the XOR technique can actually be slower than using a temporary variable for swapping because a modern CPU strive to execute instructions in parallel via instruction pipelines. In the XOR technique, the following inputs are highly dependent on each previous operation, so they must be executed in strictly sequential order, negating any benefits of instruction-level parallelism. Also, modern compilers apply any optimization necessary so both of these swaps are done with the similar amount of work. So I wouldn’t sweat about which method to use in reality, but it is important to understand the concept so you would correctly apply it when its necessary to use.
